070-2015

MO640 - Multiple-choice question

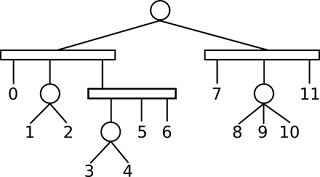
To test for the C1P on a connected component of the strict overlap graph, we need to keep a linear order (called Path in the figure below) of twin classes, and update the structure with each new set added.

Suppose that a certain number of sets have been processed, with the C1P being satisfied so far, and  arriving at the structure shown below.



When adding a new set S, the current classes can be classified into three categories:

•  empty (no elements in common with S),
•  full (contained in S), or
•  partial (some, but not all, ements contained in S).

 Adding set S = {3, 4, 8, 9} to this data structure: 

1. ... the C1P would be destroyed because there is a twin class of new elements but not a suitable extremity in the path to place it.
2. ... the C1P would still hold true.
3. ... the C1P would be destroyed because some class is partial and there is no empty neighbour or free extremity to place the subclass disjoint from S.
4. ... the C1P would be destroyed because the updated classes contained in S do not form a consecutive block.
5. None of the above.

Original idea by: Celso A. W. Santos

069-2015

MO640 - Multiple-choice question

When testing for the C1P on a connected component of the strict overlap graph, one startegy is to keep a linear order of twin classes for the sets already processed, and update this structure for each new set added.

Suppose a correct twin-class path for an already processed subfamily that has the C1P is as follows:

 

 Which of the following sets would violate the consecutive ones property if added?

1. {1, 3, 6, 7}
2. {2, 7}
3. {3, 4, 6}
4. {4, 5, 7, 8}
5. None of the above.

Original idea by: Juan Felipe Hernández Albarracín

068-2015

MO640 - Multiple-choice question

Call T(U) the collection of the trivial subsets of U.
The complete collection of C = {bfg, cdef, abcd} under U = abcdefg is:

a) T(U) ∪ {ab, abcd, abcdef, abcdfg, acd, bcdefg, bfg, bg, cd, cde, cdef, ef, fg}
b) T(U) ∪ {ab, abcdef, abcdfg, bcdefg, bdfg, bg, cd, cde, cdef, ef, efg, fg}
c) T(U) ∪ {abcd, abcdef, abcdfg, acd, bcdfeg, bfg, cde, cdef}
d) T(U) ∪ {abcdef, abcdfg, bcdfeg}
e) None of the above

Original idea by: Miriam Ito

077-2007

MO640 - Multiple-choice question

Considering the PQR tree below, which of the alternatives contains sets that do NOT belong to the tree's complete collection?

a) { M N } and { M O }
b) { C D } and{ K L }
c) { A B }, { J K }, and { L M }
d) { E F G }, { G H }, and { H I }
e) None of the above.

Original idea by: Daniel M. Ivasse
Translation help by: Mario Akita

067-2015

MO640 - Multiple-choice question

To test for the C1P on a connected component of the strict  overlap graph, we need to keep a linear order of twin classes for the sets already processed, and update this structure as each new set is added.

Suppose we are processing the following sets in the order they are given below:

S1 = {1,4}
S2 = {1,3,5}
S3 = {3,2,5}
S4 = {1,3,2}

Mark the CORRECT option describing what happens when set S4 is added.

a) The C1P is destroyed because there is no suitable location to place the class {5} that was split from an existing class.
b) The C1P is destroyed because there is no suitable location to place the class {2} that was split from an existing class.
c) The C1P is destroyed because there is no suitable location to place the class {3} that was split from an existing class.
d) The C1P is destroyed because not all updated classes contained in S4 can be kept consecutive.
e) None of the above.

Original idea by: Raphael Cristofaro 

076-2007

MO640 - Multiple-choice question

Choose the WRONG alternative regarding PQ-Tree and PQR-Tree:

1. Every PQ-Tree is a PQR-Tree, but the reverse is not true.
2. The children of an R node can be freely permuted in equivalente transformations, and the same holds for Q nodes.
3. Intersection, disjoint union and noncontained complement are operations that can be used to calculate the completion of a set family.
4. There is always a PQR-Tree that represents a finite family of restrictions over a finite universe.
5. None of the Above.

Original idea by: Celmar Guimarães da Silva
Translation help by: Andrey Victor Justo

114-2008

MO640 - Multiple-choice question

Let C = { abcd, bcdef, afghijk, bcdgh, ghijk }. Choose the alternative that contains all nontricial sets of twins from C:

1) abc, gh, ijk
2) bcd, ef, hij
3) bcd, gh, ghi
4) bcd, gh, ijk
5) None of the above

Author: Victor de Abreu Iizuka
Translation help by: Rafael S. Padilha

069-2007

MO640 - Multiple-choice question

 Which alternative is NOT equivalent to the PQ-tree in Figure 1

 
Figure 1

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. None of the above
   

Original idea by: Paulo Renato de Faria

066-2015

MO640 - Multiple-choice question

Which of PQ-trees below is not equivalent to the following PQ-Tree?

A)	B)
C)	D)
E) None of the above

Original idea by: Cristiano Borges Cardoso

065-2015

MO640 - Multiple-choice question

Consider the PQ-tree below:

Which of the following is NOT a permutation consistent with the given PQ-tree?

a) ABDFEHGC
b) ACDEGFHB
c) BHGFEDAC
d) CHGEFDAB
e) None of the above

Original idea by: Miriam Ito

074-2007

MO640 - Multiple-choice blog

Regarding PQ-Trees, select the incorrect option:

1. In a proper PQ-Tree, every element U appears as a leaf exactly once.
2. A frontier corresponds to the reading of all leaf nodes from left to right.
3. Equivalent trees have the same frontier.
4. In a universe of n elements, the space used by a PQ-Tree is linear and limited to 2n nodes.
5. None of the above

Original idea by: Lucas Pedersen Parizzi
Translation help by: Cicero Silva Luiz Junior

064-2015

MO640 - Multiple-choice question

With respect to the PQ-tree below, which alternative contains a set S such that the pruned pertinent subtree for S is a proper PQ-Tree over a subset of U = {0,1,2,...,11}?

1. {0, 1, 2, 5, 6}
2. {7, 8, 10, 11}
3. {1, 2, 3, 4, 5, 6}
4. {7, 8, 9, 10}
5. None of the above.

Original idea by: Juan Felipe Hernández Albarracín

105-2008

MO640 - Multiple-choice question

In a PQ-tree, when we are adding a new restriction, which of the following statements is true?

   a. If a node is partial, then none of its children is full
   b. If a node is partial, then none of its children is pertinent
   c. If a node has any of its children empty, then it must be an empty node
   d. If a node has any of its children full, then it must be a pertinent node
   e. None of the above

Original idea by: Priscila Nascimento Biller
Translation help by: Leandro José de Bortoli

063-2015

MO640 - Multiple-choice question

According to the concept of equivalence transformations by Booth and Lueker (1976), which alternative DOES NOT represent a PQ-tree equivalent to the following tree?

a)	b)
c)	d)
e) None of the above

Original idea by: Leandro Tacioli

062-2015

MO640 - Multiple-choice question

Given the PQ-tree T below, analyze the statements:

I) FRONTIER(T) is the permutation ABCDEFGHIJKLMNOP.
II) CONSISTENT(T) has 14496 permutations.
III) T is PERTINENT(T,S) if S={A,B,G,K,M}
IV) T is PRUNED (T,S) if and only if S contains all the leaves of the tree.

Which statements are correct?

a) IV, only
b) I and III, only
c) I, III, and IV, only
d) II, III and IV, only
e) None of the above

Original Idea by: Mario Akita

078-2007

MO640 - Multiple-choice question

Which of the alternatives below is incorrect?

1. The null tree is not considered a PQ tree;
2. To obtain the frontier of a PQ tree we have to read the tree leaves from left to right;
3. Reversing the children of a P node is an equivalence transformation;  
4. Reversing the children of a Q node is an equivalence transformation;
5. None of the above 

Original idea by: Moacy Barros Correia da Silva
Translation help by: Jessica Akemi Matsuoka

106-2008

MO640 - Multiple-choice question

Given the PQ-tree below, which of the following permutations is consistent with it?

1. ACDEGFB
2. DEFGABC
3. GACEDFB
4. GFEDBCA
5. None of the above.

Original idea by: Fabio L. Usberti

Translation help by: Wesley Ide

108-2008

MO640 - Multiple-choice question

Which of the statements below are true about Booth and Lueker's linear-time algorithm to build a PQ-tree:

I - The algorithm has two steps: one to identify the nodes that must be processed and another to apply the reductions.
II - Every child of a Q node has a pointer to its parent
III - The linear complexity can be confirmed by amortized analysis

A. I and II
B. I and III
C. II
D. III
E. None of the above

Original idea by: Maria Angélica Lopes de Souza
Translation help by: Rafael Soares Padilha

061-2015

MO640 - Multiple-choice question

Find the connected compontents in the strictly overlapping graph for the clones x probes matrix below.

L1	0	1	0	0	0	1	0	1	0	0
L2	0	0	1	0	1	0	1	0	0	0
L3	0	0	1	1	0	0	1	0	0	0
L4	1	0	0	0	0	0	0	0	1	0
L5	1	0	0	0	0	0	0	1	1	0
L6	0	0	1	0	0	0	1	0	0	1
L7	0	0	0	0	0	0	0	1	0	0

a)		b)
c)		d)

e) None of the above

Original idea by: Miriam Ito